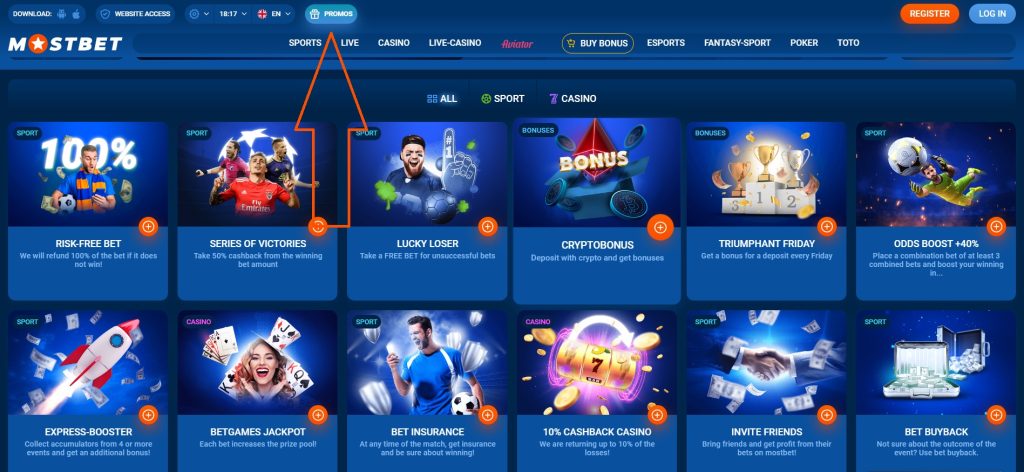
PROMO EYLEM
Risksiz Bahis
Seçilen maçlara risksiz bahisler yapın! Kaybederseniz kazanın veya bahsinizin %100'ünü iade edin!
StarBet NV’nin sahibi olduğu Mostbet bahis şirketi 2009 yılından beri Türkiye ve Azerbaycan pazarında faaliyet göstermektedir . Dünyanın 92 ülkesinde, 8048/JAZ2016-065 numaralı lisans altında, resmi web sitesi aracılığıyla çevrimiçi olarak çalışır. Kurumda kara noktası bulunmamaktadır. Sitenin 2 bölümü vardır: spor, yani bahisçi ve kumarhane.
Mostbet
Mostbet’teki oranların etkinliği ortalamadır, marj 10’dur, katalogda sırasıyla 24+ spor için etkinlikler mevcuttur, herhangi bir oyunda ödeme% 95 olabilir. Herhangi bir oyuncunun %95’lik ödemesini alabileceğinin garantisi olarak, büyük liglerde futbol üzerine 85 tür bahis kabul edilmektedir:
Kullanıcılar tarafından 5/5 olarak derecelendirildi:
Minimum depozito miktarı 10$’dır. İkmal, bahisçinin web sitesinde kişisel hesabınızda bir başvuru oluşturduktan hemen sonra gerçekleştirilir. Para ikmali / para çekme için ödeme sistemleri mevcuttur:
Para çekme, kişisel hesabınız üzerinden de gerçekleştirilir – “Hesaptan para çekme” – yöntemi, hesap numarasını – “Sipariş ödemesi” belirtin. Para, bakiyeyi yenilemek için daha önce daha iyi kullanılan ayrıntılara gelecek. Terim, birkaç dakikadan 72 saate kadar ödeme sisteminin türüne bağlıdır.
Önemli! Para çekmeden önce, 1.3 katsayısını belirterek bahislerde ikmalinizin miktarını girin veya bu para için herhangi bir slotta, sanal sporda veya canlı kumarhanede bir kumarhanede oynayın.
Bahis şirketi futbola odaklanmıştır, site tüm önemli olayları takip eder – maçlar, şampiyonalar, yerel toplantılar, Premier Lig.
Mostbet web sitesinin arayüzü uygundur, şirket logosunun üst kısmında bir ayarlar menüsü ve diğer işlevsel sekmeler bulunur:
![]()
Sayfanın ana kısmı, spor etkinliklerinin bulunduğu bir tablo tarafından işgal edilmiştir, solda, simgelerin bulunduğu şeridin altında bir yan menü gizlenmiştir. Ev Sahibi ve Yaklaşan bölümlerine ek olarak (zaman içindeki en son spor etkinliklerini gösterir), 6 alt bölümlü Futbol:
İsimlerin olduğu listeden seçim yaparak maçları ülke bazında izleyebilirsiniz. “Futbol”/”Kulüpler” bölümü – etkinliklerin bulunduğu tablonun üzerinde yer alır, aramayı daraltmak için “CANLI” ve “Hat”ı seçebilirsiniz. Veya takımın adına göre – arama çubuğundaki rekabet türü.
![]()
Eklentiler menüde “Diğer” simgesinin altında gizlidir:
CS:GO ve diğer oyunlarda takımların müsabakalarını takip edebilirsiniz, bahisçinin sanal sporları (futbol, rugby, voleybol, 10’dan fazla çeşidi vardır.
Sağda bir bahis kuponu var, sayfanın altında bilgi sekmeleri var (Hakkımızda, kurallar, kişiler, mobil versiyon, ortaklık programı, SSS – popüler soruların cevapları ile birlikte). Aşağıda ödeme sistemlerinin logoları, popüler futbol kulüplerinin isimleri ve sitenin mobil sürümünü indirmek için “İndir” butonu yer almaktadır.
Site lisanslıdır, modern bir şifreleme sistemi sayesinde, kaptanın verileri üçüncü şahısların erişemeyeceği bir yerde güvendedir.
Bahis yapabilirsiniz:
Kimin kazanacağı ve kimin telafi edebileceği ve kaç puanla ilgili tahminler yapın. Savaşta ordudan ve muharebelerden bahsetmekten kaçınmak önemlidir, bu tür konular yasal olarak çalıştığı için kurumun notunu olumsuz etkiler.
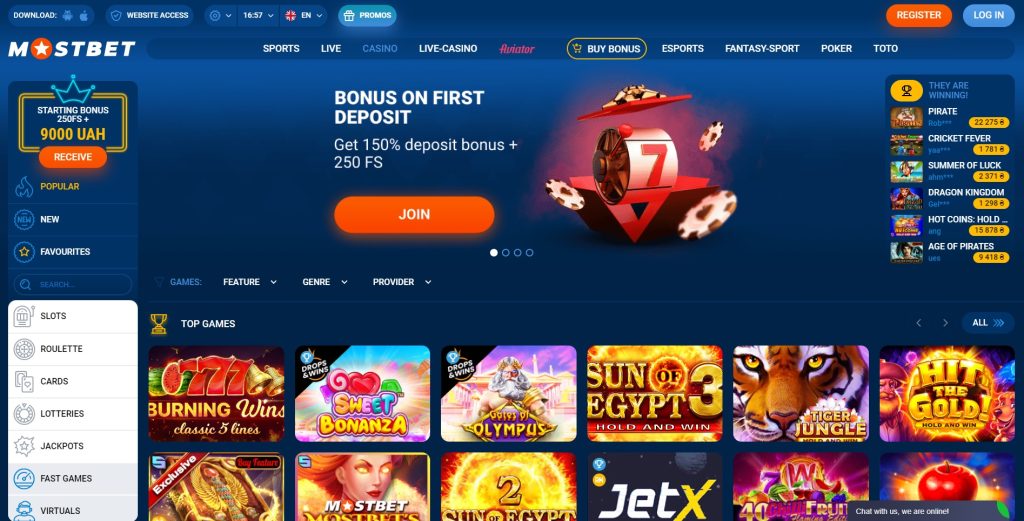
Mostbet, yeni ve düzenli oyuncular için birçok bonus sunar. Hoşgeldin bonusu, bahisçinin ofisinin misafirlerinin aşağıdakilere hızla alışmasına yardımcı olur:
Kumarhanede para iadesi de% 10’dur. Bahis şirketi, önemli tatil tarihlerinde düzenli olarak promosyonlar düzenlemeye devam etmektedir, haberlerden haberdar olmak için kayıt olmanız ve hemen haber bültenine abone olmanız gerekir. Aktif oyuncular, risksiz bahis + ücretsiz bahis sigortasına erişebilir. Doğum günü hediyeleri veriyorlar.
Sunulan tüm bonuslardan yararlanmak için platforma kayıt olmanız ve Mostbet’te mevcut olan herhangi bir yöntemi kullanarak bakiyenizi yenilemeniz gerekir. Yeni başlayanlara 1-4 depozito için “çörekler” verilir, minimum miktarda kısıtlamalar vardır. Koşullar karşılandıktan sonra hediyeler otomatik olarak kredilendirilecektir.
| Marka | Mostbet |
| Resmi site | mostbet.com |
| Ayna | https://www.openbugs.net/ |
| Kurtuluş tarihi | 2009 yılı |
| Lisans | Kurasao |
| Mal sahibi | CMS Trust NV aracılığıyla StarBet NV |
| Oyun türleri | Spor Bahisleri, Canlı Bahisler, Casino Oyunları, Canlı Casino, Aviator, Esports, Poker |
| oyun sayısı | 3700+ |
| Alan | %6-7 |
| Diller | RU, EN, UZ, AZ, TR, HI, IR, UA, KZ, ES, EN, FR, UR, HY, AG, BR, BY, CZ, PL, RO, PE, BD, NO, PT, CL |
| Ülkeler | tüm dünya |
| yasak coğrafyalar | ABD, Fransa, İngiltere, İspanya ve İtalya |
| ödeme sistemleri | Visa, Mastercard, Maestro, MIR, Visa Qiwi Wallet, Neteller, Piastrix, Webmoney, Skinpay, ecoPayz; Beeline, Megafon, Tele2 ve MTS, Bitcoin, Litecoin, Ripple ve Ethereum |
| para birimleri | AED, TÜMÜ, AMD, AUD, AZN, BDT, BND, BRL, BYN, CLP, CNY, COP, CZK, DKK, EUR, GBP, GEL, GHS, HRK, HUF, IDR, ILS, INR, IRR, JPY, KES, KHR, KRW, KZT, mBT, MKD, MNT, MXN, MYR, NGN, NOK, PEN, PHP, PKR, PLN, RON, RSD, RUB, RWF, SEK, SGD, THB, TWD, TZS, UAH, UGX, USD, UZS, VND, XAF, XOF, ZAR |
| dak. Depozito | 5$ |
| dak. ödemek | 10$ |
| Aylık para çekme limiti | 2000$ |
| promosyon kodu | IGRA150 |
| para yatırma bonusu | 500$ + 250 FS |
| Para | h60 |
| Destek | [email protected] |
| kumarhane platformu | Sahip olmak |
Bahisçinin ofisi, bahis dünyasında rahat etmek ve büyük mali kayıplar olmadan stratejisini oluşturmak isteyen yeni başlayanlar için uygun bir platform haline gelecek. Minimum bahis birdir ve tüm sistem için geçerlidir – 10$. Maksimum – faktörlerin etkisi altındaki değişiklikler:
Örneğin FIFA, Barcelona ya da bir dizi NBA playoff maçına bazen 1.000.000$ bahis yapılır ve bu limit değildir. Yerel olaylar daha az alakalıdır.
Sağ üst köşede yer alan “Kayıt Ol” butonuna tıklayarak siteye 4 şekilde kayıt olabilirsiniz. Konuğun uygun seçeneği seçeceği bir form açılacaktır:
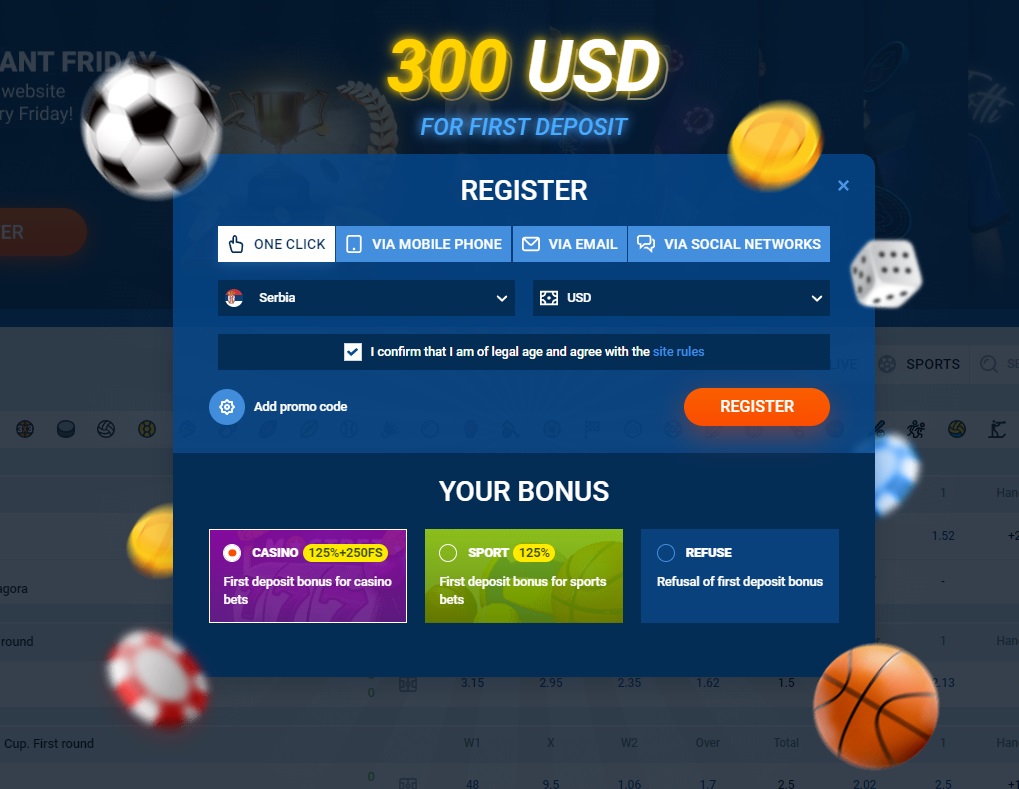
Bahis şirketi, güvenlik kurallarının bir parçası olarak, yeni oyuncunun pasaport/ehliyet sayfalarının ve e-cüzdan sayfasının/banka kartı taraflarının taranmış kopyalarını sağlayarak kimliğini doğrulamasını isteyecektir. Tüm veriler, kimlik avı ve diğer ihlal riskini önleyen modern protokoller olan SSL ve TLS ile korunmaktadır.
Telefon numarasını / posta kutusu adresini / sosyal ağı doğrulamak gerekir, kodlu bir doğrulama SMS’i alır, kayıttan sonraki 72 saat içinde girilmelidir.
Sitede, iOS ve Android cihazlar için platformun mobil sürümünü indirebilirsiniz. İşlevsellik, tarayıcı sürümüyle neredeyse aynıdır, aşağıdaki seçenekler mevcuttur:
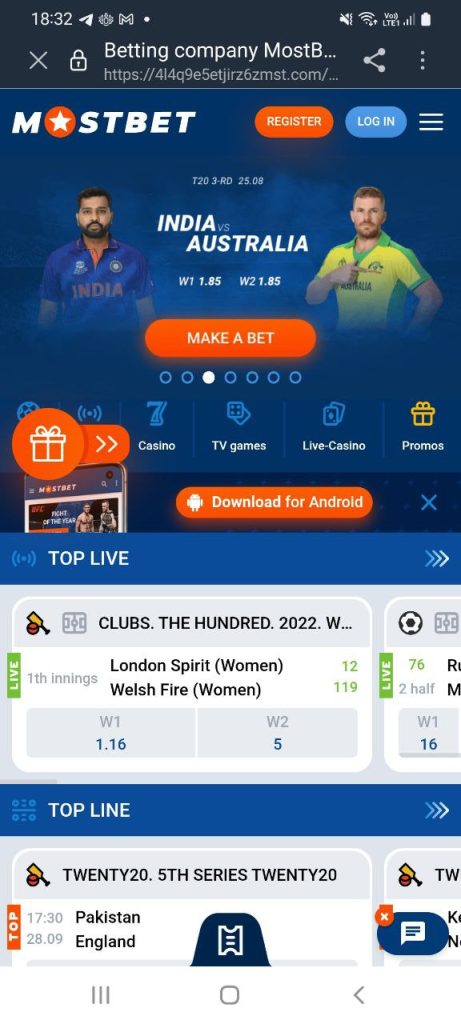
Eksi – tüm video yayınları mevcut değil, optimizasyon ortalama, cihazın teknik özelliklerine bağlı, maç sonucu yok, bölümleri ve önizlemeleri izleyebilirsiniz. Arama filtreleri ile arama yapın. Hızlı uygulamalar mevcuttur, hesabınızla giriş yapabilirsiniz.
Mostbet müşterileri, mevcut iletişim yöntemlerinden herhangi birini seçerek bir bahisçinin veya kumarhanenin çalışmaları hakkında her türlü soruyu destek servisine sorabilir:
En hızlı yanıt sohbettir. İletişim olağan – “Merhaba” ile başlayabilir ve bir cevap bekleyebilir, sorular sorabilir. Operatörler her zaman sahadadır, site yüküne bağlı olarak 1-2 dakika içinde yanıt verirler. 7/24 ulaşılabilir.
Mostbet’in çalışmasının işlevselliğini ve diğer yönlerini değerlendirdikten sonra, hizmetin avantajlarını vurgulayabiliriz:
Mostbet, reytingler, transferler ve oyuncularla ilgili en son haberleri alabileceğiniz bir Telegram kanalına sahiptir. Neredeyse tüm önemli olaylar spor dünyasıyla bağlantılıdır. Oyuncuların transferlerini beğendim – Perdue, Laporte, Joan, Juzez, Garman, Juventus. Maçlardaki galibiyet duyuruları, yarılar, bahis maçları, basın bültenleri, FIFA, orta saha oyuncuları, maçlar – en iyi ve yerel, kazanmak veya berabere oynamak, Premier Lig. Makaleler düzenli olarak günde 1-2 kez yayınlanmaktadır.
Sitenin ana sayfasında, aynı adlı kumar kuruluşuna gidebileceğiniz bir “Kumarhane” sekmesi vardır. Katalog, Playson, Spinomenal, Pragmatic Play ve diğer lisanslı operatörlerin slotlarını içerir. Yeni başlayanlar için başlangıç bonusu 250 bedava dönüş + 500$. slotların yanı sıra rulet ve kart oyunları (bakara, poker, blackjack) ve canlı krupiyeli canlı oyunlar da bulunmaktadır. Yetki gerekli değildir, bahisçi ve kumarhane aynı sitede yer almaktadır.
Mostbet, tüm oyunculara sadık bir bahis şirketidir. Herhangi bir ödeme sistemine hızlı para çekme işleminden çok memnun kaldım. Kumarhanede ayrıca lisanslı slotlar vardır, bu da hayranlar için büyük bir artıdır.
Herkese selam! Mostbet adamları ödemeyi tam bir hafta erteledi, durumu düzeltmeme yardım edin. Web sitenizde IGRA150 promosyon koduyla bir bonus aldınız